楊輝三角形,又稱賈憲三角形、帕斯卡三角形、海亞姆三角形,是二項式係數在的一種寫法,形似三角形,在中國首現於南宋楊輝的《詳解九章算術》得名,書中楊輝說明是引自賈憲的《釋鎖算術》,故又名賈憲三角形。
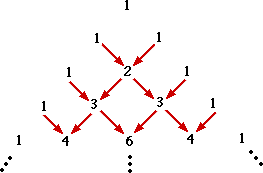
由圖我們可很明顯的找出規律性:
一、每列都比前列多一個數
二、每數都是前列的二數和
三、頭、尾項都為1
四、由網路資料可得知這樣的規律性剛好是 (a+b)n
二元一次表達式的展開系數表
| (a+b)0 = |
1
|
1
|
| (a+b)1 = |
a+b
|
1
1
|
| (a+b)2 = |
a2+2ab+b2
|
1
2 1
|
| (a+b)3 = |
a3+3a2b+3ab2+b3
|
1
3 3 1
|
| (a+b)4 = |
a4+4a3b+6a2b2+4ab3+b4
|
1
4 6 4 1
|
| (a+b)5 = |
a5+5a4b+10a3b2+10a2b3+5ab4+b5
|
1
5 10 10 5 1
|
| (a+b)6 = |
a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6
|
1
6 15 20 15 6 1
|
再參考了這篇資料: 巴斯卡三角形的幾個性質
看完後,只能說搞數學的不簡單能找出這麼多東西出來,也提供了公式,
但公式的東西實在很難看懂,有時覺得很簡單的原理,看了論文的公式,
反而覺得好複雜。
但瞭解越多資訊,越有助解題。
下列代碼,利用了第c[0]項跟最後一項c[-1]都為1,第c[1]項開始剛好等於前列r-1的c[n]+c[n-1]的和
# python
def pascalTriangle(n): if n <= 0: return else: row = [1] for i in range(10): print row p = row[:] # p 代表前一列 for j in range(1, len(row)): row[j] = p[j] + p[j-1] row.append(1) if __name__ == "__main__": pascalTriangle(10)
列印結果如下:
========================
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]
[1, 6, 15, 20, 15, 6, 1]
[1, 7, 21, 35, 35, 21, 7, 1]
[1, 8, 28, 56, 70, 56, 28, 8, 1]
[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]
沒處理空白問題,這樣代碼較方便理解
另外從網路看另一種利用zip的解法
def pascal(n): """Prints out n rows of Pascal's triangle. It returns False for failure and True for success.""" row = [1] k = [0] for x in range(max(n,0)): print row row=[l+r for l,r in zip(row+k,k+row)] return n>=1
第二列開始
row = [1, 1]
zip(row+[0], [0]+row) -> [(1, 0), (1, 1), (0, 1)]
[(1, 0), (1, 1), (0, 1)] 每項tuple再相加 -> [1, 2, 1]
第三列開始 row = [1, 2, 1]
zip(row+[0], [0]+row) -> [(1, 0), (2, 1), (1, 2), (0, 1)]
[(1, 0), (2, 1), (1, 2), (0, 1)] 一樣相加 -> [1, 3, 3, 1]
最後為練習kotlin 我再將代碼,轉換為kotlin的寫法
// kotlin code
fun pascalTriangle(n: Int) { var row = listOf(1) var k = listOf(0) if (n <= 0) { return } for (i in 1..n) { row.forEach {print("${it.toString().format(5)} ")} println() row = (row+k).zip(k+row) map {it -> it.first + it.second} } } fun main(args: Array<String>) { pascalTriangle(10) }
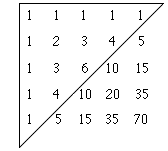
沒有留言:
張貼留言